682. Сумма на отрезке

Задан набор чисел a₁, ..., a_n. Для заданных индексов l и r найдите

Вход. В первой строке записано количество чисел n (1 ≤ n ≤ 10⁶). Во второй строке записаны числа a_i (1 ≤ a_i ≤ 1000), разделенные пробелом. В третьей строке записано количество запросов m (1 ≤ m ≤ 10⁶). Далее на отдельных строках записаны сами запросы l_i и r_i (1 ≤ l_i ≤ r_i ≤ n).

Выход. Выведите в отдельных строках m чисел S_li..ri.

Пример входа	Пример выхода
5 1 2 3 4 5 5 1 5 2 3 3 4 2 5 1 4	15 5 7 14 10

РЕШЕНИЕ

частичные суммы

Анализ алгоритма

Каждый запрос S_l,r можно выполнять при помощи цикла за время O(n). Имеется m ≤ 10⁶ запросов, длина массива составляет n ≤ 10⁶. При линейном времени выполнения запроса нам потребуется не более n * m ≤ 10¹² операций, что даст Time Limit.

Рссмотрим частичные суммы массива а:

s₁ = a₁;

s₂ = a₁ + a₂;

s₃ = a₁ + a₂ + a₃;

. . .

s_n = a₁ + a₂ + a₃ + . . . + a_n;

Вычислить значения s₁, s₂, …, s_n можно в линейном массиве s за время O(n).

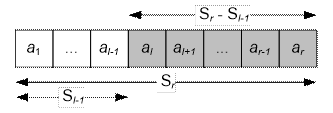
Далее заметим, что

S_l,r = a_l + a_{l + 1} + … + a_r =

= (a₁ + … + a_l + a_{l + 1} + … + a_r) – (a₁ + … + a_l-1) = s_r – s_l-1

Таким образом ответить на запрос S_l,r можно за O(1), то есть за константное время.

Пример

Вычислим сумму a₃ + a₄ + a₅ для приведенного в условии примера.

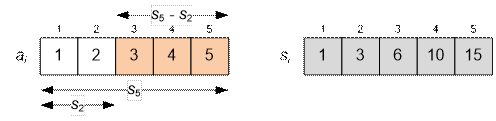
Имеем: a₃ + a₄ + a₅ = s₅ – s₂ = 15 – 3 = 12.

Реализация алгоритма

Объявим два рабочих двумерных массива.

#define MAX 1000001

int a[MAX], s[MAX];

Читаем входной набор чисел в массив a, вычисляем частичные суммы в массиве s.

scanf("%d",&n);

s[0] = 0;

for(i = 1; i <= n; i++)

{

scanf("%d",&a[i]);

s[i] = s[i-1] + a[i];

}

Обрабатываем m запросов.

scanf("%d",&m);

for(i = 0; i < m; i++)

{

scanf("%d %d",&b,&c);

printf("%d\n",s[c] - s[b-1]);

}

Реализация алгоритма – SQRT декомпозиция - TLE

#include <cstdio>

#include <cmath>

#include <vector>

using namespace std;

int i, n, m, len, x, y;

vector<int> a, b;

int q(int l, int r)

{

int i, sum = 0;

int c_l = l / len, c_r = r / len;

if (c_l == c_r)

for (i = l; i <= r; i++)

sum += a[i];

else

{

for (i = l; i <= (c_l + 1)*len - 1; i++)

sum += a[i];

for (i = c_l + 1; i <= c_r - 1; i++)

sum += b[i];

for (i = c_r * len; i <= r; i++)

sum += a[i];

}

return sum;

}

int main(void)

{

scanf("%d", &n);

a.resize(n);

for (i = 0; i < n; i++)

scanf("%d", &a[i]);

len = sqrt(n) + 1;

b.resize(len);

for (i = 0; i < n; i++)

b[i / len] += a[i];

scanf("%d", &m);

for (i = 0; i < m; i++)

{

scanf("%d %d", &x, &y);

printf("%d\n", q(x - 1, y - 1));

}

return 0;

}

Реализация алгоритма – запрос за линейное время - TLE

#include <stdio.h>

#define MAX 1000001

int i, j, n, m, b, c, s;

int a[MAX];

int main(void)

{

scanf("%d", &n);

for (i = 1; i <= n; i++)

scanf("%d", &a[i]);

scanf("%d", &m);

for (i = 0; i < m; i++)

{

scanf("%d %d", &b, &c);

s = 0;

for (j = b; j <= c; j++)

s = s + a[j];

printf("%d\n", s);

}

return 0;

}

Python реализация

Читаем входные данные.

n = int(input())

a = [0] + list(map(int, input().split()))

В списке s вычисляем частичные суммы списка а.

s = [0] * (n + 1)

for i in range(1, n + 1):

s[i] = s[i - 1] + a[i]

Обрабатываем m запросов.

m = int(input())

for _ in range(m):

b, c = map(int, input().split())

print(s[c] - s[b - 1])